Pythagorean theorem calculator

Formula: a² = b² = c²

a =

b =

c =

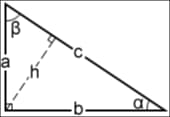
Pythagorean theorem

The Pythagorean theorem is a fundamental principle in mathematics that relates to right-angled triangles. It establishes a relationship between the lengths of the three sides of a right triangle, specifically the two shorter sides and the longest side. This theorem is named after the ancient Greek mathematician Pythagoras, who is credited with its discovery.

According to the theorem, in any right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides. This can be expressed mathematically as a Pythagorean equation:

c^{^}2 = a^{^}2 + b^{^}2

Where c represents the length of the hypotenuse, and a and b represent the lengths of the other two sides (legs) of the right triangle. The theorem holds true for all right triangles, regardless of their size or proportions.

The theorem has numerous practical applications in various fields, including geometry, physics, engineering, and architecture. Use our Pythagorean calculator for an in-depth understanding and a quick solution.

Algebraic proof

There are several algebraic proofs of the Pythagoras theorem, each utilizing different algebraic techniques to demonstrate its validity.

Consider a right triangle with legs of lengths a and b, and a hypotenuse of length c. By drawing an altitude from the right angle to the hypotenuse, it divides the triangle into two smaller triangles. These triangles are similar to the original right triangle, as they share the same angles.

Using the similarity of triangles, we can set up proportions. The ratio of the length of the altitude to the length of the corresponding portion of the hypotenuse is equal in both smaller triangles. This can be expressed as (a/x) = (x/b), where x represents the length of the altitude.

Simplifying the proportion gives x^{^}2 = ab.

Next, we add the areas of the two smaller triangles to find the area of the larger triangle. The area of each smaller triangle is given by (1/2)(a)(x) and (1/2)(b)(c - x), respectively. Summing these areas yields (1/2)(a)(x) + (1/2)(b)(c - x) = (1/2)(c)(c), which simplifies to ax + bx - ab = (1/2)(c^{^}2).

Rearranging the equation gives ax + bx = (1/2)(c^{^}2) + ab, and factoring out x yields (a + b)x = (1/2)(c^{^}2) + ab.

Since (a + b) is equal to c, we can substitute c for (a + b) in the equation, resulting in cx = (1/2)(c^{^}2) + ab.

Finally, simplifying further leads to c^{^}2 = a^{^}2 + b^{^}2, which is the Pythagorean theorem.

This algebraic proof demonstrates the relationship between the sides of a right triangle using proportions, areas, and algebraic manipulation. Gain a comprehensive understanding and find quick solutions using our Pythagoras calculator.