Surface area calculator
Ball surface area
Radius (r)
meters
Cone surface area
Base Radius (r)
meters
Height (h)
meters
Cube surface area
Edge Length (a)
meters
Cylindrical tank surface area
Base Radius (r)
meters
Height (h)
meters
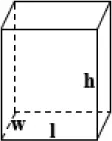
Rectangular tank surface area
Length (l)
meters
Width (w)
meters
Height (h)
meters
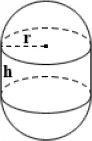
Capsule surface area
Base Radius (r)
meters
Height (h)
meters
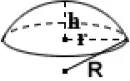
Cap surface area
Please provide any two values below to calculate.
Base Radius (r)
meters
Ball Radius (R)
meters
Height (h)
meters
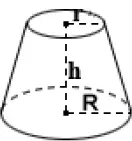
Conical frustum surface area
Top Radius (r)
meters
Bottom Radius (R)
meters
Height (h)
meters
Ellipsoid surface area
Axis 1 (a)
meters
Axis 2 (b)
meters
Axis 3 (c)
meters
Square pyramid surface area
Base Edge (a)
meters
Height (h)
meters
Surface area
In mathematics, we use the term surface area to talk about the total space that the outside of an object takes up. It's kind of like how much wrapping paper you'd need to completely cover a gift if that gift were a geometric shape!
For example, imagine you have a sphere, like a perfectly round ball. To calculate the sphere surface area, you use the formula 4πr². In this formula, 'r' is the sphere's radius. That's like a line drawn from the very center of the sphere straight out to its surface.
Now, consider an ellipsoid. This shape is similar to a sphere, but it's been stretched or squished along its different dimensions. Working out the ellipsoid surface area is a bit trickier and usually involves a bit more advanced maths, using something called integral calculus.
Lastly, think about a square pyramid. This is a 3D shape with a flat square base and four triangular sides. The formula for the square pyramid surface area is a bit more complicated: it's the area of the base plus half the product of the base's perimeter and the slant height (so 1/2perimeterslant height).
So, in short, the surface area is all about figuring out how much space the outside of an object takes up.
Sphere
You know when you have a perfectly round ball, like a football or a globe, and you wonder how much space the entire outer surface takes up? That's what we call sphere surface area in maths!
Imagine you have a football right in front of you. The average football has a radius of about 4.5 inches (that's the distance from the very center of the ball to the outer surface).
We're going to use the formula for the surface area of the sphere, which is 4πr², to find out how much space the entire outer surface of the football takes up. In this case, 'r' stands for radius, which we've already established is about 4.5 inches.
So, plug in those numbers: 4 * π * (4.5)². When you calculate this, it comes out to approximately 254.47 square inches.
So, if you lay out the football flat's surface, it would cover an area of around 254.47 square inches!
Calculating cone surface area is a bit trickier because you've got a flat circle on one end and a curved surface wrapped around the sides.
Cone
Think about a cone, like an ice cream cone. If you ever wondered how much wrapping paper you'd need to completely cover it, you're pondering its cone surface area! Unlike a cube, where the cube surface area is simply six times the area of one side, cones are a bit trickier.
We calculate the cone's surface area by adding the areas of its base and side. So, imagine an ice cream cone with a radius of 3 inches and a height of 4 inches. To figure out the lateral surface area (that's the curved part, like the wrapper of the ice cream), we use the formula πr√(r² + h²). Plug in our numbers and we get π3√(3² + 4²). That gives us approximately 37.68 square inches.
Cube
Consider a cube, like a Rubik's cube in your hand. To know how much paint you'd need to cover it, you'd need to calculate its cube surface area.
It's simply six times the area of one of its faces. So, imagine a cube with an edge length of 4 inches. To determine the surface area, use the formula 6a², where a is the edge length. Substitute your value into the formula, and you get 6*4², which equals 96 square inches.
Cylindrical tank
Picture a cylindrical tank, like a water tank in your backyard. If you wished to paint it all over, you'd need to know the surface area of the cylindrical tank. Unlike a rectangular box, a cylindrical tank's surface isn't just the sum of its sides.
To find the surface area, we sum the areas of its two circular bases and its curved body. Suppose you have a tank with a radius of 2 meters and a height of 3 meters. Use the formula 2πrh + 2πr², where r is the radius and h is the height. Plug in your values to get approximately 62.83 square meters.
Rectangular tank
Imagine a rectangular tank just like a shoebox. Suppose you want to wrap it completely, you need to calculate the surface area.
The surface area of a rectangular tank is the sum of the areas of all six faces. Let's take a tank having length (l) 4 meters, width (w) 3 meters, and height (h) 2 meters. The surface area is calculated as SA = 2lw + 2lh + 2wh.
Replacing these dimensions, we get SA = 243 + 242 + 232. The surface area of our tank, thus, is 56 square meters. That means, you'd need enough wrapping paper to cover 56 square meters to fully wrap this tank.
Different from a cone surface area, the surface area of a rectangular tank offers a simpler calculation, highlighting the applicability of geometry in real-world situations, making learning more relatable and fun for students.
Capsule
Envision a capsule, similar to a pill. To determine how much material you need to completely cover it, you calculate its surface area.
The surface area of a capsule is a bit trickier than a cube surface area. It comprises two hemispheres and a cylinder. Let's take a capsule with a hemisphere radius (r) of 2 cm and a cylindrical height (h) of 6 cm. The surface area is computed as SA = 4πr² + 2πrh.
Substituting the values, we get SA = 4π2² + 2π2*6. Thus, the surface area of our capsule is 8π + 24π, which equals 32π square cm, or approximately 100.53 square cm.
So, to create a capsule coating, we would require material enough to cover approximately 100.53 square cm. Unlike a cube, calculating the surface area of a capsule introduces students to the exciting complexity and diversity in geometry.
Spherical cap
Let's imagine a spherical cap, something akin to the scoop of ice cream that sits atop a cone. If you desired to decorate this scoop with sprinkles, the sprinkles would represent the surface area you need to cover. The calculation is different from the square pyramid surface area, given the unique shape of the spherical cap.
To find the surface area of a spherical cap, we need to know its radius and height. Let's say our ice cream scoop has a radius of 2 cm and a height of 1.5 cm. The formula for the surface area is 2πrh, where r is the radius and h is the height. Substituting the values, we find the surface area is approximately 18.85 square cm.
Remember, although the sprinkles metaphor helps make this concept relatable, the application is vast. Understanding surface areas of different shapes prepares you for diverse problems in the worlds of science, architecture, and more!
Conical frustum
Let's visualize a conical frustum, which is essentially a cone with its top lopped off. When considering painting it, determining the surface area becomes vital. This process is unlike calculating the ellipsoid surface area, given the frustum's unique geometry.
In order to calculate the surface area of a conical frustum, we need to know the radii of the top and bottom bases, along with the slant height. Suppose our frustum has top and bottom radii of 3 cm and 5 cm respectively, with a slant height of 10 cm. The formula for surface area is πr₁s + πr₂s + π(r₁ + r₂)√((r₂ - r₁)² + h²), where r₁ and r₂ are top and bottom radii, h is height and s is slant height.
Substituting these values, we get approximately 264.91 square cm. Understanding this concept not only benefits in painting frustums, but also when dealing with various geometrical problems, including ellipsoid surface area calculations!
Ellipsoid
Picture an ellipsoid, similar to a squished sphere. Wondering about the amount of paint needed to fully cover it? You're asking about its ellipsoid surface area! Unlike a square pyramid surface area, where you add up the base area and four triangle areas, an ellipsoid's calculation needs a bit more finesse.
You determine the ellipsoid's surface area using an equation involving its three different radii - a, b, and c. For instance, if a, b, and c all equal 3 units, the surface area can be found using the formula 4π[(a²b² + a²c² + b²c²)/3]^(1/2). Inserting our radii, we compute 4π[(3²3² + 3²3² + 3²3²)/3]^(1/2), giving around 113.1 square units.
Ellipsoids, like all 3D shapes, have unique surface area formulas. Just as you work out a square pyramid's or cone's surface area, understanding these calculations deepens your knowledge of geometric shapes.
Square pyramid
Square pyramid is like the one you'd see on a classic Egyptian landscape. If you ever considered how much paint you'd need to cover all its sides, then you're exploring the square pyramid surface area.
To calculate the square pyramid's surface area, we add the area of its base to the area of its four triangular sides. So, imagine a pyramid with a base length of 5 units and a slant height of 7 units.
For the base, the formula is simple: it's just the square of the base length (5²), which equals 25 square units. For the sides, each triangle's area is 0.5 times the base length times the slant height (0.557), and since there are four identical triangles, we multiply this by 4.
Doing the calculation gives us 70 square units for the triangular sides. Adding the base area, the total surface area of our square pyramid is 25 + 70 = 95 square units.
Common area units
| Unit | meter2 |
| centimeter2 | 0.0001 |
| millimeter2 | 0.000001 |
| micrometer2 | 0.000000000001 |
| hectare | 10,000 |
| mile2 | 2,589,990 |
| yard2 | 0.83613 |
| foot2 | 0.092903 |
| inch2 | 0.00064516 |
| acre | 4,046.86 |